머신러닝을 이해하기 위한 첫 번째 수학적인 지식이다. 선형 연립 방정식 파트는 이후 수학적 용어 이해를 돕기 위한 과정으로 생각하면 된다.
1. 선형 연립 방정식
1) Norm : 원점벡터와 벡터의 거리 (벡터의 크기)
- Norm은 크기의 일반화로 벡터의 크기(혹은 길이)를 측정하는 방법
- 두 벡터 사이의 거리를 측정하는 방법
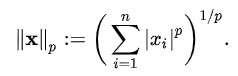
- p = Norm의 차수
- p = 1, L1 Norm
- p = 2, L2 Norm
- n = 해당 벡터의 원소 수
- L1 norm


- L2 norm
- 가장 짧은 직선의 거리


- norm은 벡터를 input으로 갖고, output은 벡터의 거리 크기를 나타낸다.
2) 직교성
- x,y 벡터에 대한 inner product가 0이면 수직이다.

- 각각의 벡터의 크기가 1이면 x,y 벡터가 수직이다.

3) 두 벡터 사이 각도


4) Halfspace


- 바깥쪽 법선 벡터 y와 경계 0의 뒷쪽에 있는 모든공간이 x집합에 해당된다.
5) 선형변환
- Superposition(중첩)과 Homogeneity(균질성)를 만족할 때 선형변환이라고 부른다.
- 선형변환은 행렬로 표현할 수 있다.
- Superposition : 중첩


- input에서 먼저 sum을 하고 선형변환하는 것과 input에서 먼저 선형변환을 하고 sum을 하는 것이 같을 때
- Homogeneity : 균질성


- input에서 실수배를 하고 선형변환을 진행하는 것과 선형변환을 먼저 진행하고 실수배를 하는 것이 같을 때
6) 회전변환
- Rotation Matrix : M = R(θ)

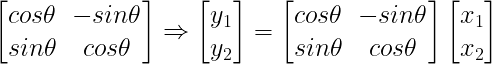




- 회전행렬 M = R(θ) 찾기
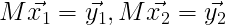


7) 투영변환

x축으로 투영변환

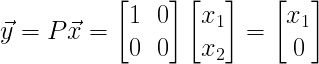
<실습>
실습 1



import numpy as np
A = np.array([[4,-5], [-2,3]])
b = np.array([[-13], [9]])
x = np.linalg.inv(A).dot(b)
print(x)
[[3.]
[5.]]
실습 2

x = np.array([[1], [1]])
y = np.array([[2], [3]])
x.T.dot(y)
array([[5]])
실습 3

c = np.array([[3], [5]])
np.linalg.norm(c,1)
8.0
실습 4



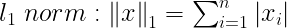

np.linalg.norm(c,2)
5.8309518948453
728x90
'머신러닝 > 머신러닝 이론' 카테고리의 다른 글
| 머신러닝 기초 수학 6 - 추가적인 수학적 개념 (0) | 2022.11.17 |
|---|---|
| 머신러닝 기초 수학 5 - 최적화와 볼록 최적화 (0) | 2022.11.17 |
| 머신러닝 기초 수학 4 - 최소자승법 (1) | 2022.11.16 |
| 머신러닝 기초 수학 3 - 다원 일차 연립방정식 (0) | 2022.11.16 |
| 머신러닝 기초 수학 2 - 고유치와 고유벡터 (0) | 2022.11.16 |
