머신러닝 기초 수학 5 - 최적화와 볼록 최적화

5. 최적화와 볼록 최적화

---

<최적화 모델 참고>

• 최적화 문제를 풀 땐 모델링을 하고 최적화의 해를 풀어야한다.

- 수학적 표준 모델

- 등가변환

---

1) 최적화 표준모델

• 이번 장은 최적화된 표준모델에 대해 알아보고 최적의 해를 구하는 과정에 대해 설명한다.
• 기본요소 : 목적함수, 변수, 제약조건

<최적화의 종류>

• (제약조건이 있는 것 vs 없는 것) + 볼록 최적화

 

2) 볼록 최적화 (Convex Optimization)

• 볼록 함수 : convex function
• 볼록 셋 : convex set

 

- 두 점 사이의 선형 보간

• convex optimization 장점 : local solution을 global solution으로 다가가는 방식이기에 최적화 문제에 중요한 솔루션이다! 대부분의 머신러닝 문제는 convex optimizer로 해결이 가능하다
• 해결과정 예시 : Machine Learning Problem => convex optimizer 인 경우=> CVXPY => approximate solution

<convex Function>

• 아래 파란 동그라미가 위의 파란 동그라미보다 항상 작은 형태의 볼록 형태 그래프여야 convex Function을 만족한다

<convex set, non-convex set>

 

• non-convex 해결법 : 여러번 반복

---

****<최적화 문제 풀 때 중요한 부분>****

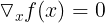
• f의 기울기가 0이 되도록 하는 x^*를 찾는 것이 중요하다!

• n차원 벡터일 때 각각의 차원에 대해 편미분을 해 모든 축 방향으로의 기울기를 계산한다.

• 따로 constained optimization이 없을 때 이와 같은 식이 만족한다.

---

<Gradient> => Gradient를 이용한 볼록최적화 문제 해결 법

Gradient 문제 1

<1> affine Function

<2> quadratic Function

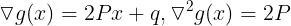
<3> g(x) = ||Ax+b||^2

 

Gradient 문제 2

 

 

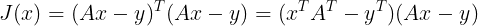
<Gradient로 미분해서 최적 해 찾기>

<이차계획법>

 

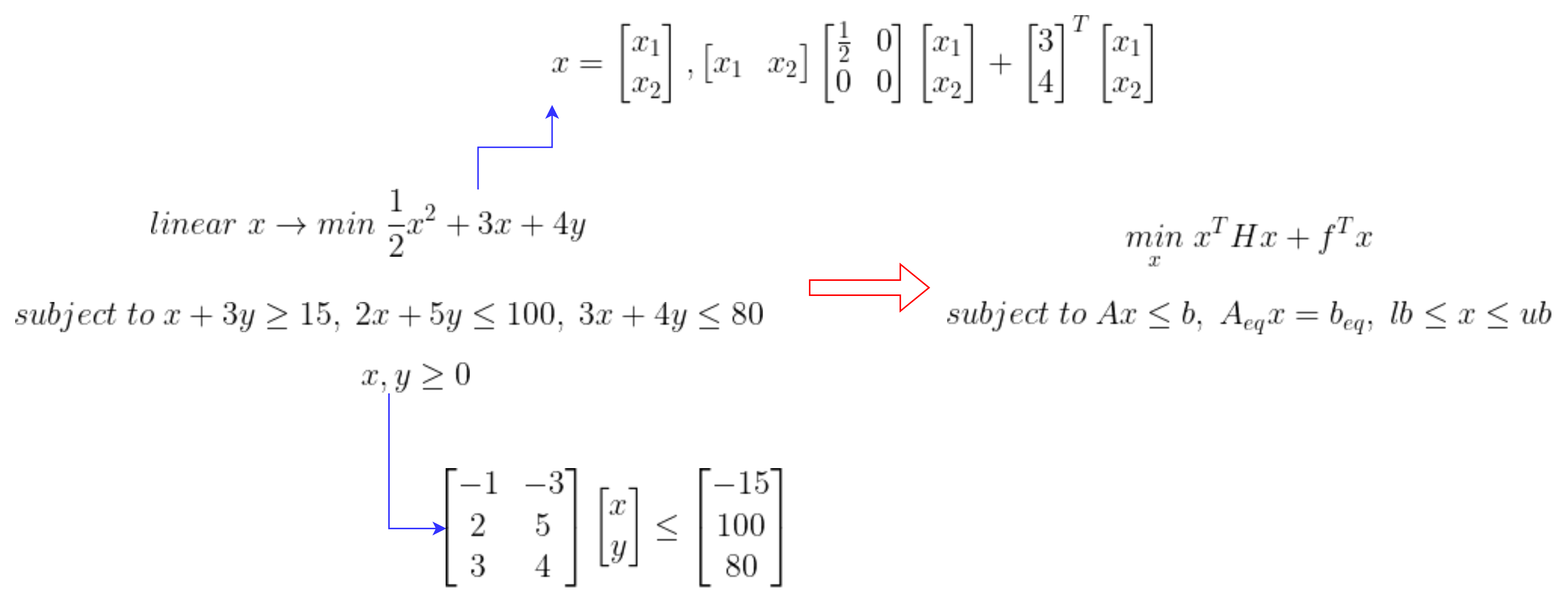
3) 경사하강법

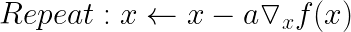
4) 이차형식, 이차계획법

• 다차항을 표현하는 기법은 이와같이 나타낼 수 있다.

---

<실습>

실습 1

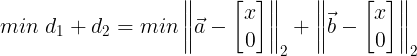
import numpy as np
import cvxpy as cvx
a = np.array([[0],[1]])
b = np.array([[4],[2]])
Aeq = np.array([0,1])
beq = np.array(0)
x = cvx.Variable(shape = (2,1))
mu = 1
obj = cvx.Minimize(cvx.norm(a-x,2)+mu*cvx.norm(b-x,2))
constraints = [Aeq*x == beq]
prob = cvx.Problem(obj, constraints)
result = prob.solve()
print(x.value)


[[1.33325114e+00]
 [5.33304239e-12]]

 

실습 2

H = np.matrix([[2,0],[0,2]])
g = -np.matrix([[6],[6]])
x = np.zeros((2,1))
alpha = 0.2
for i in range(100):
  df = H*x + g
  x = x - alpha*df
print(x)


[[3.]
 [3.]]